벨만-포드(bellman-ford-moore)
그래프에서 최단 거리를 구하는 알고리즘은 다익스트라, 벨만-포드, 플로이드 워셜이 있다. 특정 시작점에서 다른 모든 노드로의 최단 거리를 구하는 알고리즘은 다익스트라, 벨만-포드이고, 그 중 음수 간선을 다루는 유일한 알고리즘이 바로 벨만-포드이다. 그래서 코딩 테스트에서 벨만-포드가 나온다면 최단 거리보단 음수 사이클이 있는지 판단하는 문제가 더 많이 나오게 된다.
벨만-포드의 주요 특징은 다음과 같다.
| 기능 | 특징 | 시간 복잡도 (노드 수:V, 에지 수:E) |
| 특정 출발 노드에서 다른 모든 노드까지의 최단 경로 탐색 | - 음수 가중치 에지가 있어도 수행할 수 있음 - 전체 그래프에서 음수 사이클의 존재 여부를 판단할 수 있음 |
O(VE) |
벨만-포드의 핵심 이론
1. 에지 리스트로 그래프를 구현하고 최단 경로 배열 초기화하기.
출발 노드는 0, 나머지 노드는 무한대로 초기화한다. edge 클래스는 일반적으로 노드 변수 2개와 가중치 변수로 구성돼 있다.

2. 모든 에지를 확인해 정답 배열 업데이트하기.
최단 거리 배열에서 업데이트 반복 횟수는 노드 개수 - 1 이다. 노드 개수가 N이고, 음수 사이클이 없을 때 특정 두 노드의 최단 거리를 구성할 수 있는 에지의 최대 개수는 N - 1이기 때문이다. 특정 에지 E = (s, e, w)에서 다음 조건을 만족하면 업데이트를 실행한다.
업데이트 조건과 방법
D[s] != ∞ 이며 D[e] > D[s] + w 일 때 D[e] = D[s] + w로 배열의 값을 업데이트한다.

음수 사이클이 없을 때 N - 1번 에지 사용 횟수를 반복하면 출발 노드와 모든 노드 간의 최단 거리를 알려 주는 정답 배열이 완성된다. 이렇게 완성 후 마지막으로 이 그래프에 음수 사이클이 존재하는지 확인해야 한다.
3. 음수 사이클 유무 확인하기.
음수 사이클 유무를 확인하기 위해 모든 에지를 한 번씩 다시 사용해 업데이트되는 노드가 발생하는지 확인한다. 만약 업데이트되는 노드가 있다면 음수 사이클이 있다는 뜻이 되고, 2단계에서 도출한 정답 배열이 무의미하고 최단 거리를 찾을 수 없는 그래프라는 뜻이 된다. 음수 사이클이 존재하면 이 사이클을 무한하게 돌수록 가중치가 계속 감소하므로 최단 거리를 구할 수 없다.

[백준 11657번] 타임머신
https://www.acmicpc.net/problem/11657
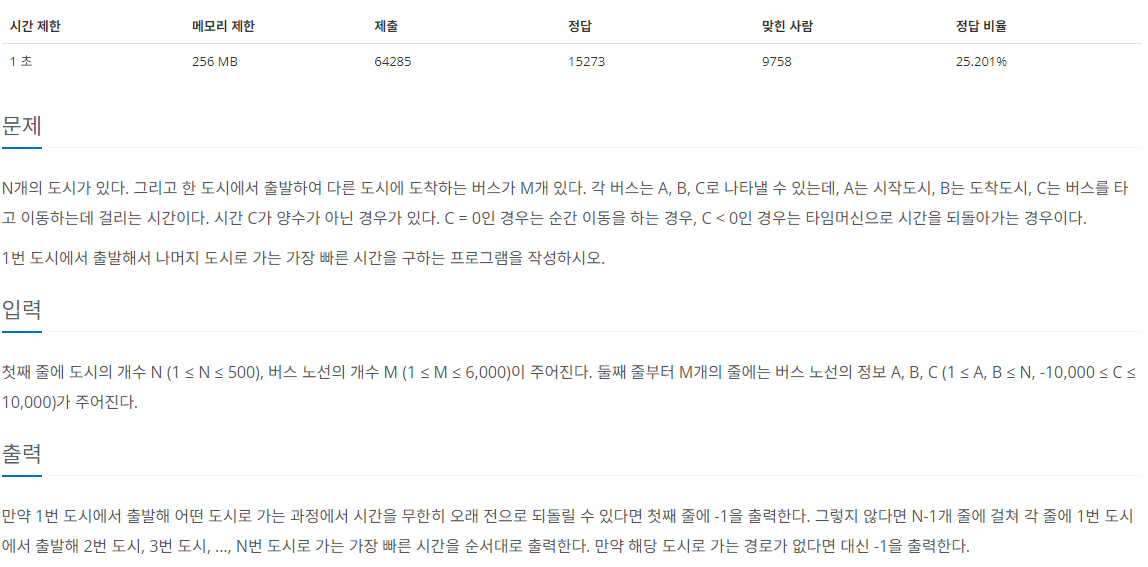
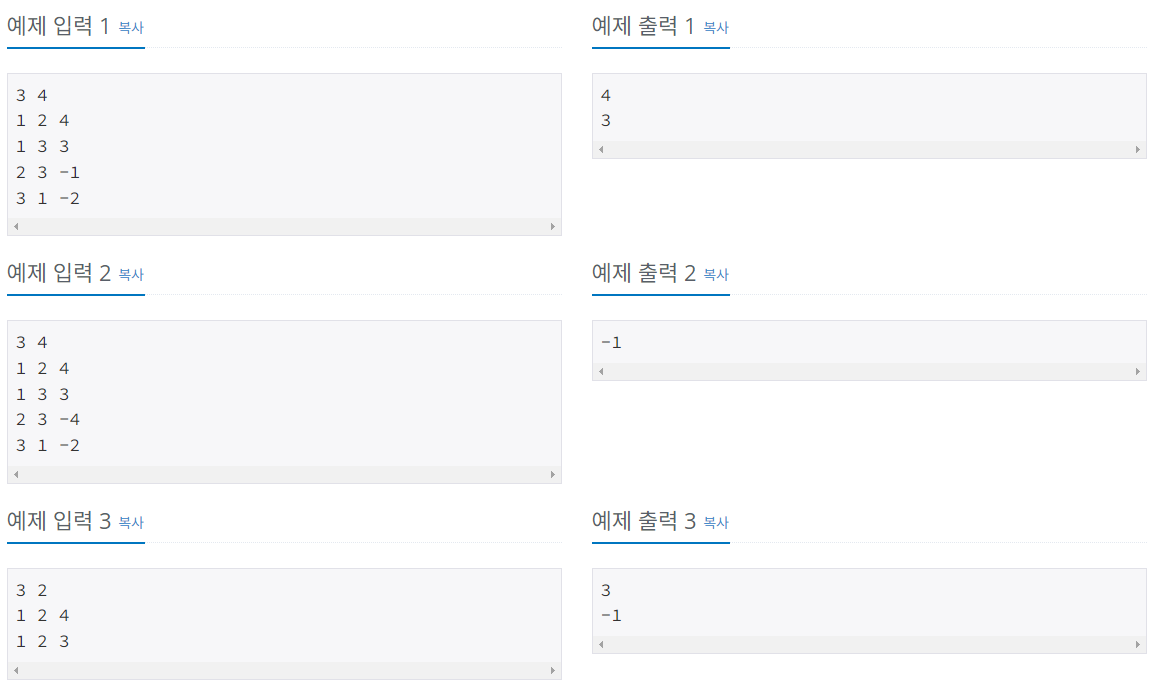
시작점에서 다른 노드와 관련된 최단 거리를 구하는데 에지가 음수가 가능할 때는 벨만-포드 알고리즘을 사용하면 된다.
1. 에지 리스트에 에지 데이터를 저장한 후 거리 배열을 다음과 같이 초기화한다. 최초 시작점에 해당하는 거리 배열값은 0으로 초기화한다.
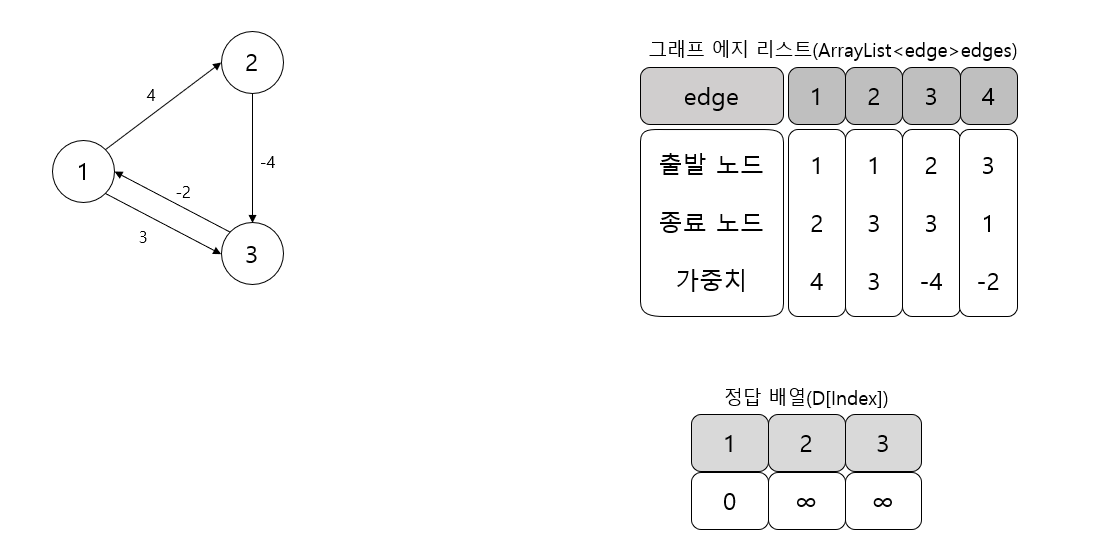
2. 다음 순서에 따라 벨만-포드 알고리즘을 수행한다.
1. 모든 에지와 관련된 정보를 가져온 후 다음 조건에 따라 거리 배열의 값을 업데이트한다.
- 출발 노드가 방문한 적이 없는 노드(출발 노드 거리 == INF)일 때 값을 업데이트하지 않는다.
- 출발 노드의 거리 배열값 + 에지 가중치 < 종료 노드의 거리 배열값일 때 종료 노드의 거리 배열값을 업데이트한다.
2. '노드 개수 - 1' 번만큼 1을 반복한다.
3. 음수 사이클 유무를 알기 위해 모든 에지에 관해 다시 한 번 1을 수행한다. 이때 한 번이라도 값이 업데이트되면 음수 사이클이 존재한다고 판단한다.
실제로 수행할 때는 에지가 저장된 순서에 따라 동작하므로 거리 배열의 값이 다음과 같이 업데이트된다. 이론의 업데이트와는 약간 다르지만, 알고리즘에 영향을 미치진 않는다. 실제 코드 디버그값과 이론에서의 값이 달라 혼동될 수 있으므로 이번에는 배열을 실제 코드 기준으로 업데이트해 보겠다.
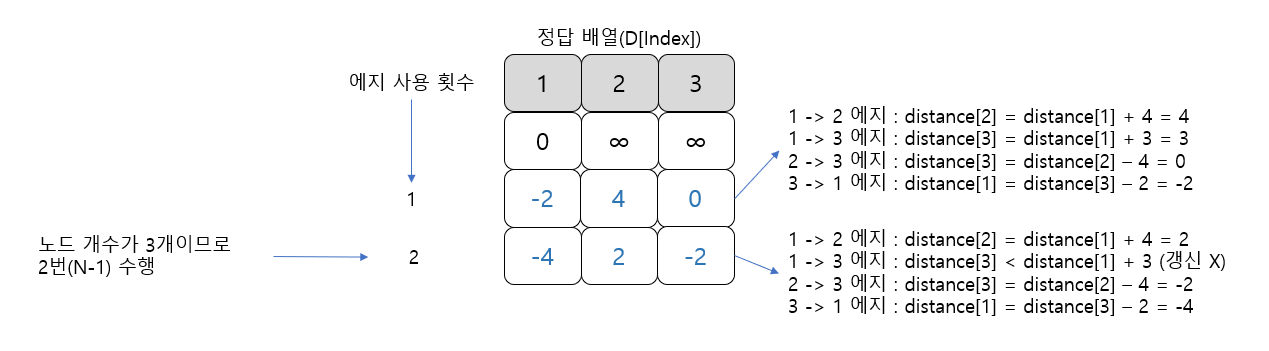
3. 음수 사이클이 존재하면 -1, 존재하지 않으면 거리 배열의 값을 출력한다. 단, 거리 배열의 값이 INF일 경우에는 -1을 출력한다.

[정답]
import java.io.*;
import java.util.*;
public class Main {
static final int INF = Integer.MAX_VALUE;
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
Edge[] edges = new Edge[M + 1];
long[] distance = new long[N + 1];
Arrays.fill(distance, INF); // 최단 거리 배열 초기화
for (int i = 0; i < M; i++) {
st = new StringTokenizer(br.readLine());
int s = Integer.parseInt(st.nextToken());
int e = Integer.parseInt(st.nextToken());
int w = Integer.parseInt(st.nextToken());
edges[i] = new Edge(s, e, w);
}
// 벨만-포드 알고리즘 수행
distance[1] = 0;
for (int i = 1; i < N; i++) { // N - 1번 만큼 반복
for (int j = 0; j < M; j++) {
Edge edge = edges[j];
// 더 작은 최단 거리가 있을 때 업데이트하기
if(distance[edge.start] != INF && distance[edge.end] > distance[edge.start] + edge.time) {
distance[edge.end] = distance[edge.start] + edge.time;
}
}
}
for (int i = 0; i < M; i++) { // 음수 사이클 확인하기
Edge edge = edges[i];
if(distance[edge.start] != INF && distance[edge.end] > distance[edge.start] + edge.time) {
System.out.println(-1);
return;
}
}
for (int i = 2; i <= N; i++) { // 음수 사이클 존재 X, 최단 거리 출력
if(distance[i] == INF)
System.out.println(-1);
else
System.out.println(distance[i]);
}
}
static class Edge { // 에지 리스트를 편하게 다루기 위해 클래스로 별도 구현
int start; // 시작점
int end; // 도착점
int time; // 걸리는 시간
public Edge(int start, int end, int time) {
this.start = start;
this.end = end;
this.time = time;
}
}
}
[백준 1219번] 오민식의 고민
https://www.acmicpc.net/problem/1219


기존 벨만-포드는 최단 거리를 구하는 알고리즘이지만, 이 문제에서는 도착 도시에 도착할 때 돈의 액수를 최대로 하고 싶기 때문에 업데이트 방식을 반대로 변경해야 한다. 또한 돈을 무한히 많이 버는 케이스가 있다고 하는 것을 바탕으로 음수 사이클이 아닌 양수 사이클을 찾도록 변경해야 한다. 그리고 마지막 예외 처리가 1개 필요하다. 바로 다음 그래프와 같이 양수 사이클이 있어도 출발 노드에서 이 양수 사이클을 이용해 도착 도시에 가지 못할 때이다.
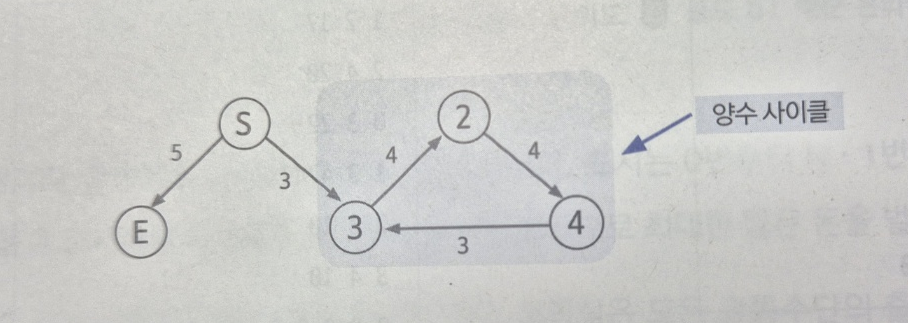
이 방법을 해결할 수 있는 방법에는 여러 가지가 있는데, 여기서는 에지의 업데이트를 N - 1번이 아닌 충분히 큰 수(도시 개수 N의 최대치 = 100)만큼 추가로 돌리면서 업데이트를 수행하도록 로직을 변경하여 해결하겠다. 이렇게 변경하는 이유는 에지를 충분히 탐색하면서 양수 사이클에서 도달할 수 있는 모든 노드를 양수 사이클에 연결된 노드로 업데이트하기 위해서이다.
1. 에지 리스트에 에지 데이터를 저장하고, 거리 배열값을 초기화한다. 최초 시작점에 해당하는 거리 배열값은 0으로 초기화한다.

2. 다음 순서에 따라 변형된 벨만-포드 알고리즘을 수행한다.
1. 모든 에지와 관련된 정보를 가져와 다음 조건에 따라 거리 배열의 값을 업데이트한다.
1-a. 시작 도시가 방문한 적이 없는 도시일 때 (시작 도시 == MIN) 업데이트하지 않는다.
1-b. 시작 도시가 양수 사이클과 연결된 도시일 때(도착 도시 == MAX) 도착 도시도 양수 사이클과 연결된 도시로 업데이트한다.
1-c. '도착 도시값 < 시작 도시값 + 도착도시 수입 - 에지 가중치' 일 때 더 많이 벌 수 있는 새로운 경로로 도착한 것이므로 값을 업데이트한다.
2. 노드보다 충분히 많은 값(N + 100)으로 1을 반복한다.

3. 도착 도시의 값에 따라 결과를 출력한다.
결과 출력 경우의 수
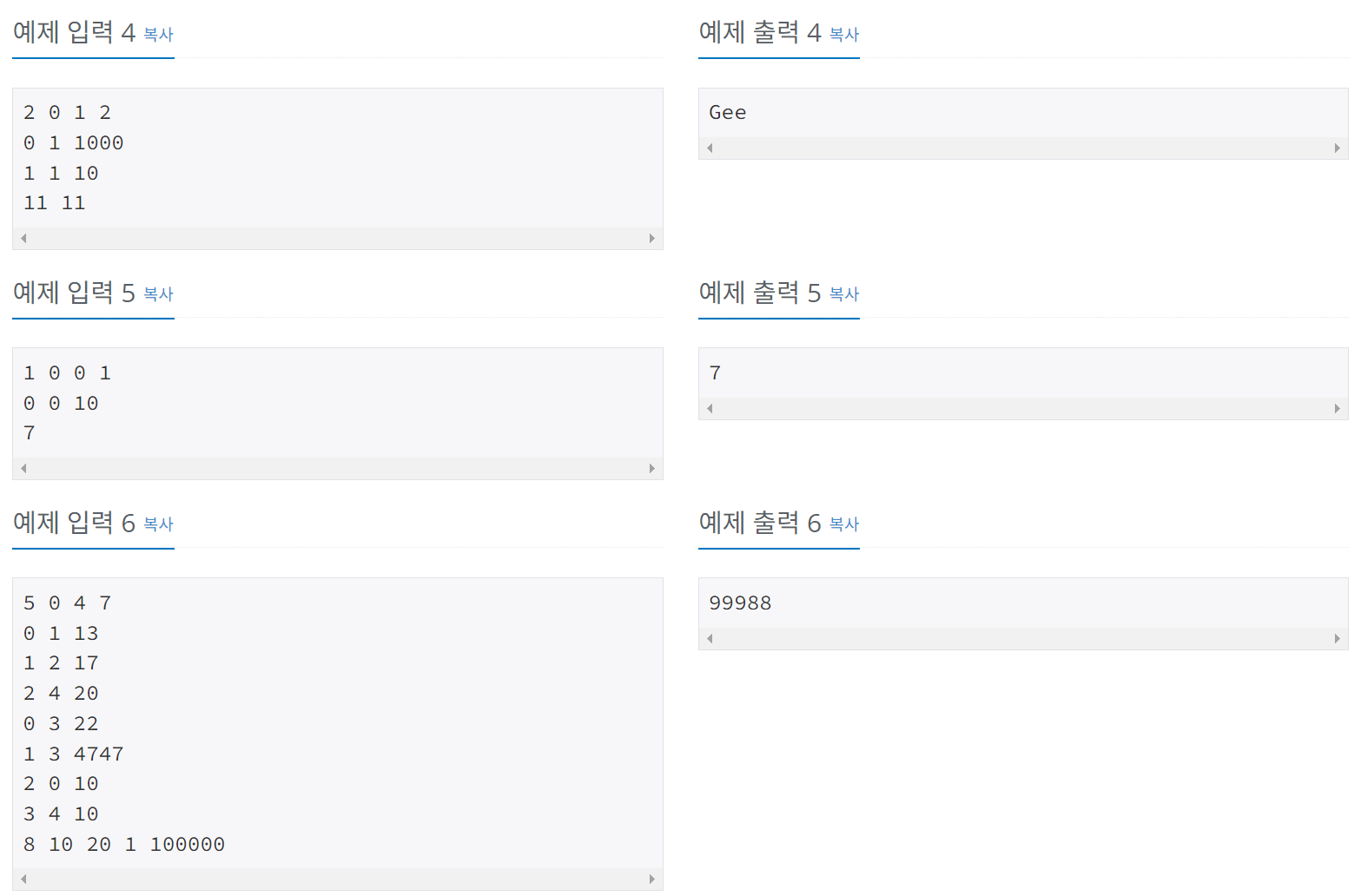
1. 도착 도시의 값이 MIN이고, 도착하지 못할 때 'gg'를 출력한다.
2. 도착 도시의 값이 MAX이고, 무한히 많이 벌 수 있을 때 'Gee'를 출력한다.
3. 이외에는 도착 도시의 값을 출력한다.

[정답]
import java.io.*;
import java.util.*;
public class Main {
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken());
int start_city = Integer.parseInt(st.nextToken());
int end_city = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
Edge[] edges = new Edge[M];
long[] distance = new long[N];
long[] cityMoney = new long[N];
Arrays.fill(distance, Long.MIN_VALUE); // 최단 거리 배열 초기화
for (int i = 0; i < M; i++) { // 에지 리스트에 데이터 저장
st = new StringTokenizer(br.readLine());
int s = Integer.parseInt(st.nextToken());
int e = Integer.parseInt(st.nextToken());
int c = Integer.parseInt(st.nextToken());
edges[i] = new Edge(s, e, c);
}
st = new StringTokenizer(br.readLine());
for (int i = 0; i < N; i++) {
cityMoney[i] = Long.parseLong(st.nextToken());
}
distance[start_city] = cityMoney[start_city]; // 변형된 벨만-포드 알고리즘 수행
// 양수 사이클이 전파되도록 충분히 큰 수로 반복
for (int i = 0; i <= N + 100; i++) {
for (int j = 0; j < M; j++) {
int start = edges[j].start;
int end = edges[j].end;
int price = edges[j].price;
// 출발 노드가 방문하지 않은 노드이면 skip
if(distance[start] == Long.MIN_VALUE) continue;
// 출발 노드가 양수 사이클에 연결된 노드라면 종료 노드도 연결 노드로 업데이트
else if(distance[start] == Long.MAX_VALUE)
distance[end] = Long.MAX_VALUE;
// 더 많은 돈을 벌 수 있는 새로운 경로가 발견됐을 때 새로운 경로값으로 업데이트
else if(distance[end] < distance[start] + cityMoney[end] - price) {
distance[end] = distance[start] + cityMoney[end] - price;
// N - 1번 반복 이후 업데이트되는 종료 노드는 양수 사이클 연결 노드로 변경
if(i >= N - 1) distance[end] = Long.MAX_VALUE;
}
}
}
if(distance[end_city] == Long.MIN_VALUE) System.out.println("gg"); // 도착 불가능
else if(distance[end_city] == Long.MAX_VALUE) System.out.println("Gee");
// 양수 사이클이 연결돼 무한대 돈 벌 수 있을 때
else System.out.println(distance[end_city]); // 이외의 경우
}
static class Edge { // 에지 리스트를 편하게 다루기 위해 클래스로 별도 구현
int start; // 시작점
int end; // 도착점
int price; // 걸리는 시간
public Edge(int start, int end, int price) {
this.start = start;
this.end = end;
this.price = price;
}
}
}
[참고 자료]
- Do it! 알고리즘 코딩테스트 자바편



