플로이드-워셜 (floyd-warshall)
그래프에서 최단 거리를 구하는 알고리즘. 주요 특징은 다음과 같다.
| 기능 | 특징 | 시간 복잡도 (노드 수: V) |
| 모든 노드 간에 최단 경로 탐색 | - 음수 가중치 에지가 있어도 수행할 수 있음. - 동적 계획법의 원리를 이용해 알고리즘에 접근 |
O(V^3) |
플로이드-워셜의 핵심 이론
플로이드-워셜 알고리즘을 도출하는 가장 핵심적인 원리는 A 노드에서 B 노드까지 최단 경로를 구했다고 가정했을 때 최단 경로 위에 K 노드가 존재한다면 그것을 이루는 부분 경로 역시 최단 경로라는 것이다.

색칠된 에지 경로가 1 -> 5 최단 경로라면 1 -> 4 최단 경로와 4 -> 5 최단 경로 역시 색칠된 에지로 이뤄질 수밖에 없다. 즉, 전체 경로의 최단 경로는 부분 경로의 최단 경로의 조합으로 이뤄진다는 의미가 된다. 이 원리로 다음과 같은 점화식 도출이 가능하다.
도출한 플로이드-워셜 점화식
- D[S][E] = Math.min(D[S][E], D[S][K] + D[K][E])
플로이드-워셜 알고리즘 구현 방법은 다음과 같다.
1. 배열을 선언하고 초기화하기
D[S][E]는 노드 S에서 노드 E까지의 최단 거리를 저장하는 배열이라 정의한다. S와 E의 값이 같은 칸은 0, 다른 칸은 ∞로 초기화한다. 여기에서 S == E는 자기 자신에게 가는 데 걸리는 최단 경로값을 의미하기 때문이다.

2. 최단 거리 배열에 그래프 데이터 저장하기
출발 노드는 S, 도착 노드는 E, 이 에지의 가중치는 W라고 했을 때 D[S][E] = W로 에지의 정보를 배열에 입력한다. 이로써 플로이드-워셜 알고리즘은 그래프를 인접 행렬로 표현한다는 것을 알 수 있다.

3. 점화식으로 배열 업데이트하기
기존에 구했던 점화식을 3중 for 문의 형태로 반복하며 배열의 값을 업데이트한다.
플로이드-워셜 알고리즘 로직
for 경유지 K에 관해 (1 ~ N) // N : 노드 개수
for 출발 노드 S에 관해 (1 ~ N)
for 도착 노드 E에 관해 (1 ~ N)
D[S][E] = Math.min(D[S][E], D[S][K] + D[K][E])

완성된 배열은 모든 노드 간의 최단 거리를 알려준다. 예를 들어 1번 노드에서 5번 노드까지 가는 최단 거리는 D[1][5] = 6으로 나타낸다.
플로이드-워셜 알고리즘은 모든 노드 간의 최단 거리를 확인해 주기 때문에 시간 복잡도가 O(V^3)으로 빠르지 않은 편이다. 그래서 일반적으로 플로이드-워셜 알고리즘을 사용해야 하는 문제가 나오면 노드의 개수의 범위가 다른 그래프에 비해 적게 나타난다.
[백준 11404번] 플로이드
https://www.acmicpc.net/problem/11404

모든 도시의 쌍과 관련된 최솟값을 찾아야 하는 문제이다. 그래프에서 시작점을 지정하지 않고, 모든 노드와 관련된 최소 경로를 구하는 알고리즘이 바로 플로이드-워셜 알고리즘이다. 도시의 최대 개수가 100개로 매우 작은 편이므로 O(N^3) 시간 복잡도의 플로이드-워셜 알고리즘으로 해결할 수 있다.
1. 버스 비용 정보를 인접 행렬에 저장한다. 먼저 인접 행렬을 초기화하는데, 연결 도시가 같으면 (i==j) 0, 아니면 충분히 큰 수로 값을 초기화한다. 그리고 주어진 버스 비용 데이터 값을 인접 행렬에 저장한다.

2. 플로이드-워셜 알고리즘을 수행한다. 다음 점화식을 활용한 3중 for 문으로 모든 중간 경로를 탐색한다.
// 두 도시의 연결 비용 중 최솟값
Math.min(distance[S][E], distance[S][K] + distance[K][E])

3. 알고리즘으로 변경된 인접 행렬을 출력한다. 인접 행렬 자체가 모든 쌍의 최단 경로를 나타내는 정답 배열이므로 정답 배열을 그대로 출력하되, 문제의 요구사항에 따라 두 도시가 도달하지 못할 때(∞)는 0, 아닐 때는 배열의 값을 출력한다.
[정답]
import java.io.*;
import java.util.*;
public class Main {
static int INF = 10000000; // 충분히 큰 수로 저장
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
int n = Integer.parseInt(br.readLine());
int m = Integer.parseInt(br.readLine());
int[][] distance = new int[n+1][n+1];
// 인접 행렬 초기화하기
for (int[] d : distance) {
Arrays.fill(d, INF);
}
for (int i = 1; i <= n; i++) {
distance[i][i] = 0;
}
for (int i = 0; i < m; i++) {
st = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
int c = Integer.parseInt(st.nextToken());
distance[a][b] = Math.min(distance[a][b], c);
}
// 플로이드-워셜 알고리즘 수행하기
for (int k = 1; k <= n; k++) {
for (int s = 1; s <= n; s++) {
for (int e = 1; e <= n; e++) {
distance[s][e] = Math.min(distance[s][e], distance[s][k] + distance[k][e]);
}
}
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
if(distance[i][j] == INF) System.out.print(0 + " ");
else System.out.print(distance[i][j] + " ");
}
System.out.println();
}
}
}
여기서 주의할 점은 INF의 값을 Integer.MAX_VALUE로 하면 이 값을 다른 값과 더하며 오버플로우가 발생해 마이너스 값이 나온다는 것이다. 최대 비용이 100,000 이니까 100001로 잡으면 틀리게 되는데, 만약 A -> B의 비용이 100000 이고 B -> C의 비용이 1이라고 했을 때 A -> C 의 경로값이 100001, 즉 INF로 인식하게 되어 버리기 때문이다. 그러므로 충분히 큰 값으로 INF를 잡아야 한다.
[백준 11403번] 경로 찾기
https://www.acmicpc.net/problem/11403
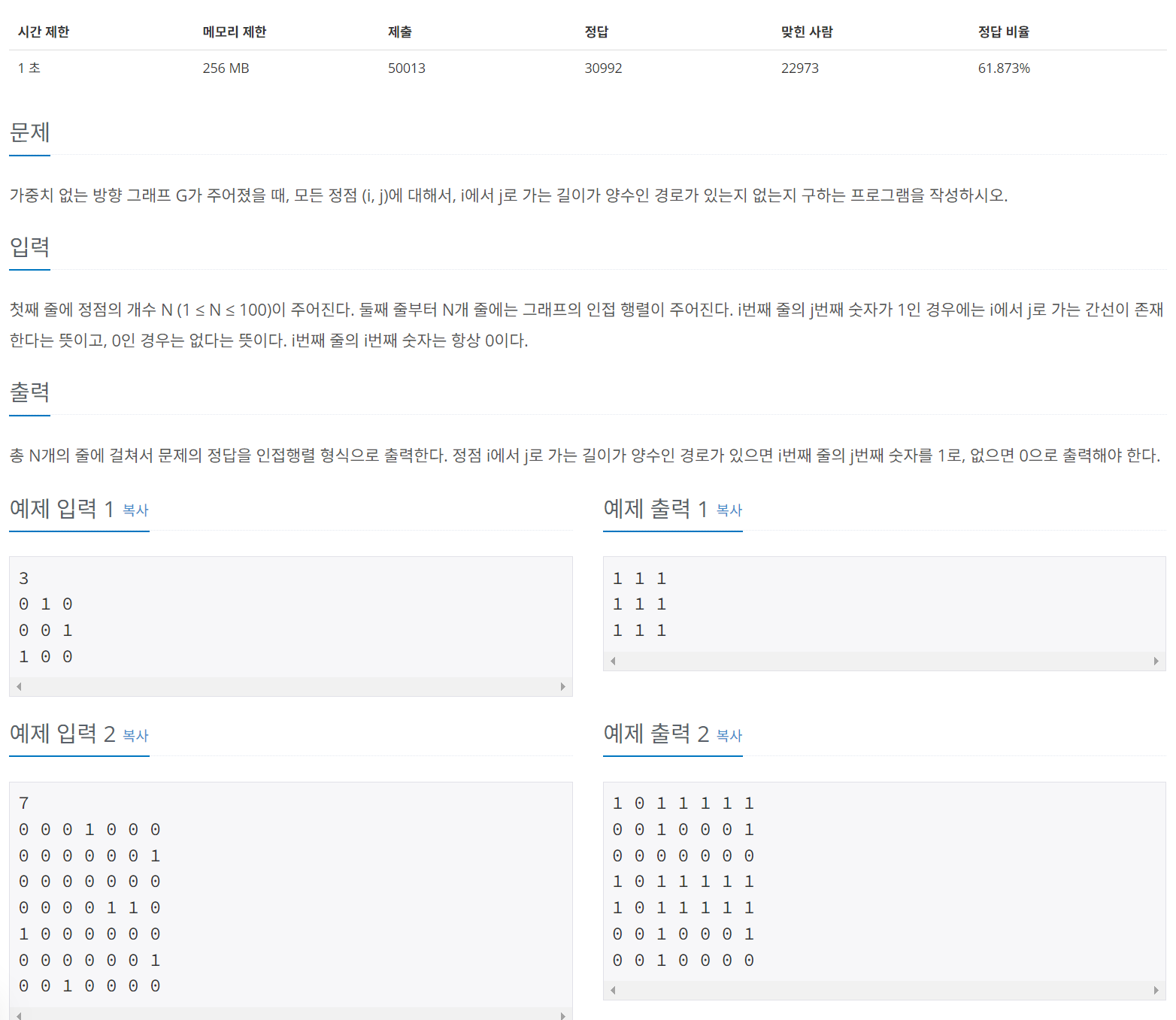
플로이드-워셜 알고리즘을 이해하고 있으면 쉽게 풀 수 있다.
[정답]
import java.io.*;
import java.util.*;
public class Main {
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
int[][] distance = new int[N + 1][N + 1];
for (int i = 1; i <= N; i++) { // 입력되는 인접 행렬의 값을 그대로 저장
StringTokenizer st = new StringTokenizer(br.readLine());
for (int j = 1; j <= N; j++) {
distance[i][j] = Integer.parseInt(st.nextToken());
}
}
for (int k = 1; k <= N; k++) { // 변형된 플로이드-워셜 알고리즘 수행
for (int s = 1; s <= N; s++) {
for (int e = 1; e <= N; e++) {
if(distance[s][k] == 1 && distance[k][e] == 1)
distance[s][e] = 1;
}
}
}
for (int i = 1; i <= N; i++) {
for (int j = 1; j <= N; j++) {
System.out.print(distance[i][j] + " ");
}
System.out.println();
}
}
}
[백준 1389번] 케빈 베이컨의 6단계 법칙
https://www.acmicpc.net/problem/1389
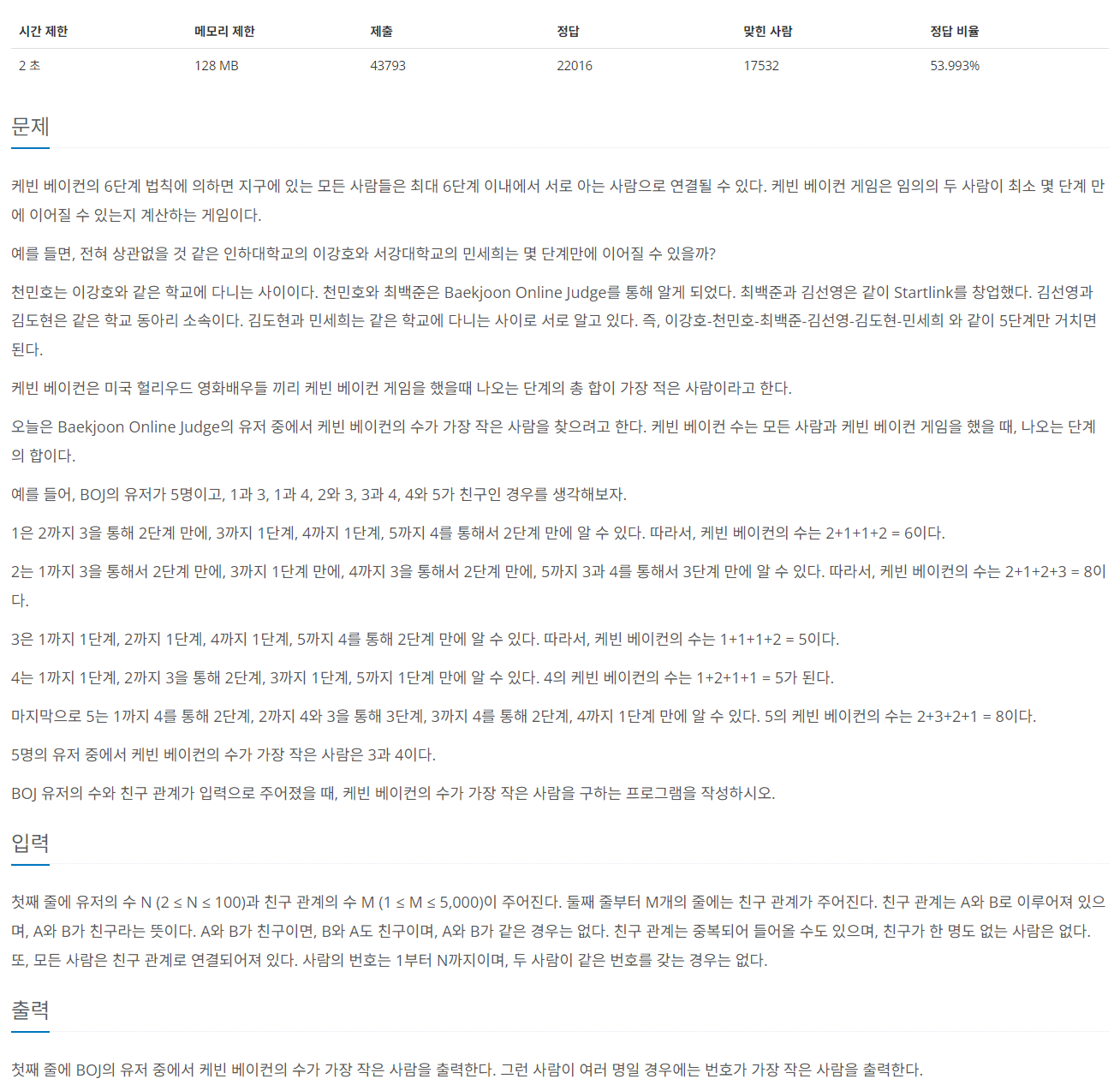

BFS 탐색 알고리즘을 이용해도 해결할 수 있는 문제이지만 유저의 최대 수가 100 정도로 작기 때문에 플로이드-워셜 알고리즘으로도 해결할 수 있다.
[정답]
import java.io.*;
import java.util.*;
public class Main {
static int INF = 100000; // 충분히 큰 수
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
int[][] distance = new int[N + 1][N + 1];
for (int i = 1; i <= N; i++) { // 인접 행렬 초기화
for (int j = 1; j <= N; j++) {
if(i == j) distance[i][j] = 0;
else distance[i][j] = INF;
}
}
for (int i = 0; i < M; i++) { // 친구 관계이므로 양방향 저장, 가중치 1로
st = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
distance[a][b] = 1;
distance[b][a] = 1;
}
for (int k = 1; k <= N; k++) { // 플로이드-워셜 알고리즘 수행
for(int s = 1; s <= N; s++) {
for (int e = 1; e <= N; e++) {
distance[s][e] = Math.min(distance[s][e], distance[s][k] + distance[k][e]);
}
}
}
int bacon = INF;
int bacon_person = -1;
for (int i = 1; i <= N; i++) {
int total = 0;
for (int j = 1; j <= N; j++) {
total += distance[i][j];
}
if(bacon > total) { // 가장 작은 케빈 베이컨의 수를 지니고 있는 i 찾기
bacon = total;
bacon_person = i;
}
}
System.out.println(bacon_person);
}
}
[참고 자료]
- Do it! 알고리즘 코딩 테스트 자바편



